By Assad Ebrahim, on January 21st, 2018 (51,387 views) |
Topic: Maths--Technical
2nd ed. January 21, 2018; 1st ed. Feb 8th, 2010
Abstract
This three part paper explores solving the sum of powers problem 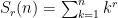 using discrete maths techniques (recurrence relations, matrix systems) to obtain a solution polynomials whose coefficients turn out to be exactly the Bernoulli numbers using discrete maths techniques (recurrence relations, matrix systems) to obtain a solution polynomials whose coefficients turn out to be exactly the Bernoulli numbers 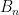 . .
Part 1 (this paper) solves the problem using recurrence relations in a way which a high school student could emulate for small  . In Part 2, we develop a general recursive solution that works for arbitrary . In Part 2, we develop a general recursive solution that works for arbitrary  , from which we can build a table of values to assist in finding the coefficients of the solution polynomial, coefficients that are precisely the Bernoulli numbers discovered in 1713. In Part 3, we show how by transforming the problem into a linear system, we may obtain a direct (non-recursive) solution which directly calculates the Bernoulli number for any power , from which we can build a table of values to assist in finding the coefficients of the solution polynomial, coefficients that are precisely the Bernoulli numbers discovered in 1713. In Part 3, we show how by transforming the problem into a linear system, we may obtain a direct (non-recursive) solution which directly calculates the Bernoulli number for any power  . Source code is provided for all solutions. . Source code is provided for all solutions.
Readers who are interested in this topic are referred also to lovely paper by Bearden (March 1996, American Mathematical Monthly), which tells the mathematical story and fills in the history (thanks to a reader for this great reference).
Continue reading this article…
By Assad Ebrahim, on January 20th, 2018 (21,216 views) |
Topic: Maths--Technical
By Assad Ebrahim, on January 19th, 2018 (12,271 views) |
Topic: Mathematics, Maths--Technical
(Discrete Mathematics Techniques III)
1st ed. Apr 2nd, 2010
Abstract
This is the last in the 3-part series of articles on finding for oneself the solution to the sum of integer power problem, and in the process discovering the Bernoulli numbers. In Part 3 (this paper), we find a direct closed-form solution, i.e. one that does not require iteration, for the general case of the finite-summation-of-integer-powers problem 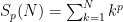 . Having established in Part 2 that the closed-form solution is a polynomial, the summation is here rewritten as the sum of the . Having established in Part 2 that the closed-form solution is a polynomial, the summation is here rewritten as the sum of the  independent monomials independent monomials 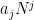 ( (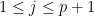 ), where the ), where the 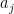 are unknown coefficients. Using the recurrence relation are unknown coefficients. Using the recurrence relation  , we obtain a linear combination of the monomials, which reduces to an easily solvable , we obtain a linear combination of the monomials, which reduces to an easily solvable 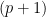 -by- -by-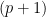 triangular linear system in the unknown coefficients triangular linear system in the unknown coefficients 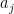 of the closed-form polynomial solution. Maxima and Octave/Matlab codes for directly computing the closed-form solutions are included in the Appendices. of the closed-form polynomial solution. Maxima and Octave/Matlab codes for directly computing the closed-form solutions are included in the Appendices.
A lovely paper by Bearden (March 1996, American Mathematical Monthly), which was shared with me by a reader, tells the mathematical story nicely, with much of the history filled in.
Continue reading this article…
By Assad Ebrahim, on January 31st, 2010 (8,085 views) |
Topic: Education, Maths--Philosophy
The mathematician Alfred North Whitehead observed that “[Advancement occurs] by extending the number of important operations which we can perform without thinking of them.” (Introduction to Mathematics, 1911 ) This is certainly true in mathematics where the development of judicious notation, accompanied by good mathematical technique, extends the capability to perform chains of complex reasoning accurately and efficiently. Through proper problem formulation (tractable yet generalizable), one can sometimes pass from a single insight to the solution of a family of problems, and in some cases, to the solution to the general question itself.
Here, mathematical computing can provide a useful benefit: helping to efficiently explore conjectures, dispatch with false directions, and save time during the development, error-checking and validation stages of obtaining general results. In industry, where specific or semi-general results are needed fast, such tools allow rapidly working up the required material and providing the necessary certainty before the fully general results or complete proof are ready.
Continue reading this article…
|
Stats: 1,066,417 article views since 2010 (March update)
Dear Readers: Welcome to the conversation! We publish long-form pieces as well as a curated collection of spotlighted articles covering a broader range of topics. Notifications for new long-form articles are through the feeds (you can join below). We love hearing from you. Feel free to leave your thoughts in comments, or use the contact information to reach us!
|
using discrete maths techniques (recurrence relations, matrix systems) to obtain a solution polynomials whose coefficients turn out to be exactly the Bernoulli numbers
.
. In Part 2, we develop a general recursive solution that works for arbitrary
, from which we can build a table of values to assist in finding the coefficients of the solution polynomial, coefficients that are precisely the Bernoulli numbers discovered in 1713. In Part 3, we show how by transforming the problem into a linear system, we may obtain a direct (non-recursive) solution which directly calculates the Bernoulli number for any power
. Source code is provided for all solutions.
