4th ed. Jan 2024; 3rd ed. May 2023; 2nd ed. Dec 2009; 1st ed. Sep 2004
“It is not philosophy but active experience in mathematics itself that alone can answer the question: `What is Mathematics?'” – Richard Courant & Herbert Robbins, 1941, What is Mathematics?, Oxford University Press)
“An adequate presentation of any science cannot consist of detailed information alone, however extensive. It must also provide a proper view of the essential nature of the science as a whole.” – Aleksandrov, 1956, Mathematics: Its Content, Methods, and Meaning
‘What is mathematics?’ Much ink has been spilled over this question, as can be seen from the selection of ten respected responses provided in the footnote, with seven book-length answers, and three written in the current millenium. One might well ask, is there anything new that can be said, that should be said? We’ll start by clarifying what a good answer should look like, and then explore the answer proposed.
The rest of the paper follows the structure below:
1. Criteria for a Good Definition of Mathematics
2. Definition 1: covering mathematics up to the end of the 18th century (1790s)
3. Two Perspectives
Mathematics as Dialectic (Lakatos)
Mathematics shaped by its Anthropology (Hoyrup)
4. Definition 2: covering all mathematics, including contemporary mathematics
5. The emergence of contemporary mathematical practice from 1800s onward
6. Three Facets of Mathematics
1. Mathematics as an Empirical Science
2. Mathematics as a Modeling Art
3. Mathematics as an Axiomatic Arrangement of Knowledge
7. Mathematics "from the inside": Mathematicians writing about Mathematics
8. Continue Reading
9. References
Continue reading this article…
2nd ed. June 2023; 1st ed. April 2010
The term “mathematical maturity” is sometimes used as short-hand to refer to a blend of elements that distinguish students likely to be successful in mathematics. It is a mixture of mathematical interest, curiousity, creativity, persistence, adventurousness, intuition, confidence, and useful knowledge.[1],[2],[3]
With advances in machine learning, computer science, robotics, nano-materials, and many other quantitative, fascinating subjects, students today have increasingly more choice in technical studies besides mathematics. To attract and retain mathematics students, it is important that mathematics instruction be experienced as both intellectually and culturally rewarding in addition to being technically empowering. Losing students from mathematics who are otherwise capable, engaged and hard-working is tragic when it could have been avoided.
In this article, building on observations gained over the years teaching and coaching students in mathematics, we consider how enriched mathematics instruction (inquiry-based/discovery learning, historiography, great ideas/survey approaches, and philosophical/humanist) can help (1) develop mathematical maturity in students from at-risk backgrounds and prevent their untimely departure from quantitative studies, (2) strengthen the understanding of those that are already mathematically inclined, (3) expand mathematical and scientific literacy in the wider population.
Continue reading this article…
By Assad Ebrahim, on January 19th, 2018 (13,335 views) |
Topic: Mathematics, Maths--Technical
(Discrete Mathematics Techniques III)
1st ed. Apr 2nd, 2010
Abstract
This is the last in the 3-part series of articles on finding for oneself the solution to the sum of integer power problem, and in the process discovering the Bernoulli numbers. In Part 3 (this paper), we find a direct closed-form solution, i.e. one that does not require iteration, for the general case of the finite-summation-of-integer-powers problem 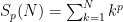 . Having established in Part 2 that the closed-form solution is a polynomial, the summation is here rewritten as the sum of the . Having established in Part 2 that the closed-form solution is a polynomial, the summation is here rewritten as the sum of the  independent monomials independent monomials 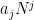 ( (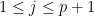 ), where the ), where the 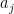 are unknown coefficients. Using the recurrence relation are unknown coefficients. Using the recurrence relation  , we obtain a linear combination of the monomials, which reduces to an easily solvable , we obtain a linear combination of the monomials, which reduces to an easily solvable 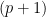 -by- -by-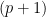 triangular linear system in the unknown coefficients triangular linear system in the unknown coefficients 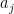 of the closed-form polynomial solution. Maxima and Octave/Matlab codes for directly computing the closed-form solutions are included in the Appendices. of the closed-form polynomial solution. Maxima and Octave/Matlab codes for directly computing the closed-form solutions are included in the Appendices.
A lovely paper by Bearden (March 1996, American Mathematical Monthly), which was shared with me by a reader, tells the mathematical story nicely, with much of the history filled in.
Continue reading this article…
By Assad Ebrahim, on July 13th, 2016 (10,993 views) |
Topic: Education
Thoughts on Teaching Mathematics in an Exploratory, Dialectical, Topical format.
(2nd ed. July 13th 2016; 1st ed. Jan 31, 2010)
Mathematics is a richly spun tapestry, threaded with interconnections from a multiplicity of endeavors, perspectives, and disciplines, both theoretical and applied. Yet contrary to this “non-linear” reality, the typical pattern of school and even university mathematics is both linear and restricted.
This article takes a look at what lies behind the way things are, and what could bring positive change.
Continue reading this article…
By Assad Ebrahim, on May 21st, 2014 (8,103 views) |
Topic: Maths--General Interest
Duelling with pistols. If you were the one issuing the challenge, your dilemma was that custom dictated that your adversary be allowed to shoot first. Only then, if you were still able to shoot, would you be permitted to seek “satisfaction”.
How much of an advantage does the first shooter really have? In this article, we build a simple probability model, and implement a numerical model in a few lines of R code.
 Two gentleman face off in the snow. Convention dictates the challenged shoots first. Continue reading this article…
By Assad Ebrahim, on April 15th, 2010 (13,665 views) |
Topic: Education, Maths--Philosophy
An examination of mathematical methods and the search for mathematical meaning.
This article curates a reading list (most sources available freely online) organized into a set of encounters that lie outside the standard mathematics curriculum. They are intended to enrich the reader’s understanding of mathematics and its place in scientific inquiry, increase her/his connection to the historical and philosophical questions behind the mathematics of the past and present, and gain greater satisfaction from further mathematical study. The reader should come away with a better understanding of the culture of mathematics: what mathematics is, mathematical method and meaning, and the relation of mathematics to the empirical world and to science.
We look at seven topics. These may be covered in any order, to suit your particular interests.
- What is Mathematics? (Its Nature and Characteristics)
- Reality, Truth, and the Nature of Mathematical Knowledge
- What is Proof? and the Problem of Certainty
- Some Readings in the History of Mathematics and the Evolution of Its Ideas
- The Search for Foundations in Mathematics
- Mathematics and Science
- Thoughts on Mathematical Practice and Mathematical Style
There is no core body of technical material to master in this course; the important thing is a feel for how, why, and in what context the core ideas of mathematics evolved, getting to the essence of their motivation, and understanding the fruits of these efforts. The course such as the below should appeal to all those who have an itch to scratch beneath the surface of mathematics, who find themselves asking “but why?”. It could be useful in all three tiers of education: secondary, post-secondary (undergraduate), and graduate, appropriately restructured.
- Secondary school elective: to encourage bright students in mathematics, science and technology to enter the university with a broader perspective on the mathematics they will be rapidly learning there.
- University elective course: offered as a writing-intensive seminar, intended primarily for students in the sciences and engineer: mathematics, physics, engineering.
- Graduate level course: offered in the first year of graduate school in mathematics or applied mathematics as a supplementary seminar.
Continue reading this article…
By Assad Ebrahim, on February 25th, 2010 (52,965 views) |
Topic: Mathematics, Maths--Technical
Updated! February 5, 2017
The value of zero raised to the zero power, 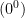 , has been discussed since the time of Euler in the 18th century (1700s). There are three reasonable choices: 1,0, or “indeterminate”. Despite consensus amongst mathematicians that the correct answer is one, computing platforms seem to have reached a variety of conclusions: Google, R, Octave, Ruby, and Microsoft Calculator choose 1; Hexelon Max and TI-36 calculator choose 0; and Maxima and Excel throw an error (indeterminate). In this article, I’ll explain why, for discrete mathematics, the correct answer cannot be anything other than 0^0=1, for reasons that go beyond consistency with the Binomial Theorem (Knuth’s argument). , has been discussed since the time of Euler in the 18th century (1700s). There are three reasonable choices: 1,0, or “indeterminate”. Despite consensus amongst mathematicians that the correct answer is one, computing platforms seem to have reached a variety of conclusions: Google, R, Octave, Ruby, and Microsoft Calculator choose 1; Hexelon Max and TI-36 calculator choose 0; and Maxima and Excel throw an error (indeterminate). In this article, I’ll explain why, for discrete mathematics, the correct answer cannot be anything other than 0^0=1, for reasons that go beyond consistency with the Binomial Theorem (Knuth’s argument).
Continue reading this article…
By Assad Ebrahim, on January 15th, 2010 (14,109 views) |
Topic: Maths--History, Maths--Philosophy
The development of mathematics has had many encouraging forces: societal, technological, cultural. These have served to accelerate mathematics and have been accelerated in turn, in many cases the pair becoming locked into a mutually beneficial resonance that has dramatically energized both.
In this article, I look at some of the significant catalysts, from the rise of the leisured class in ancient times to the impact of computing in modern times.
Continue reading this article…
By Assad Ebrahim, on January 3rd, 2010 (163,500 views) |
Topic: Maths--History, Maths--Philosophy
The development of mathematics is intimately interwoven with society and culture, influencing the course of history through its applications to science and technology.
But mathematics itself has changed much over its history. Even the mathematics of the early 1800s can now seem quite strange, so great have been the changes in just the past 150 years as it has been reworked in the modern abstract approach. Though advanced mathematics may now appear arcane from the outside looking in, the present state of mathematics is the result of a natural evolution of the subject. And there is much excitement promised ahead with the rise of new mathematics and application areas in subatomic and quantum physics, in the the field of statistical learning (also called artificial intelligence or machine learning), and in numerical computing and simulation.
What follows is the story of mathematics, in a nutshell.
Continue reading this article…
By Assad Ebrahim, on January 2nd, 2010 (115,264 views) |
Topic: Maths--Philosophy
What are the characteristics of mathematics, especially contemporary mathematics?
I’ll consider five groups of characteristics:
- Applicability and Effectiveness,
- Abstraction and Generality,
- Simplicity,
- Logical Derivation, Axiomatic Arrangement,
- Precision, Correctness, Evolution through Dialectic…
Continue reading this article…
|
Stats: 1,089,379 article views since 2010 (Aug '24 update)
Dear Readers: Welcome to the conversation! We publish long-form pieces as well as a curated collection of spotlighted articles covering a broader range of topics. Notifications for new long-form articles are through the feeds (you can join below). We love hearing from you. Feel free to leave your thoughts in comments, or use the contact information to reach us!
|

