By Assad Ebrahim, on July 7th, 2019 (14,871 views) |
Topic: Software Engineering, SWEng--Toolbox
If you haven’t done so already, you may want to start by reading the Preface to the Computing Series: Software as a Force Multiplier, Sections 1-3.
1. Total Commander: a programmable, extensible, feature-rich two-panel orthodox file manager
Total Commander (TC) is more than just a two-panel orthodox file manager for Windows. It is a swiss army knife of computing utilities and is the first piece of software that I install on any Windows computer on which I’m working. Total Commander, used well, is a force multiplier.
Tenets of the TC approach:
- Two-panes is the natural way to think about most file and directory operations (source panel, destination panel).
- Keys beats mouse for speed and accuracy. Make the keyboard use easy. List of keyboard shortcuts and description of features
- A computing platform should be fully extensibility. Adding your own tools should be easy.
- Portability secures your investment: grab your totalcmd folder, copy to a new computer, and everything should work seamlessly.
I’ve been using TC continuously since 2001. Over the years, I’ve put together a Total Commander Expansion Pack (lite and full) for the TC platform that conforms to the tenets and further extends TC platform’s capabilities with tools I have found valuable. Both are pre-configured downloads to allow unpack and start using with minimum fuss (I use them when switching computers). Feel free to download and give them a try. Feedback or questions welcomed in the comments.
 Total Commander Expansion Pack Winter 2024 – Toolbar View with Integrated Applications, Download from link. Continue reading this article…
By Assad Ebrahim, on January 19th, 2018 (14,350 views) |
Topic: Mathematics, Maths--Technical
(Discrete Mathematics Techniques III)
1st ed. Apr 2nd, 2010
Abstract
This is the last in the 3-part series of articles on finding for oneself the solution to the sum of integer power problem, and in the process discovering the Bernoulli numbers. In Part 3 (this paper), we find a direct closed-form solution, i.e. one that does not require iteration, for the general case of the finite-summation-of-integer-powers problem 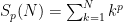 . Having established in Part 2 that the closed-form solution is a polynomial, the summation is here rewritten as the sum of the . Having established in Part 2 that the closed-form solution is a polynomial, the summation is here rewritten as the sum of the  independent monomials independent monomials 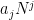 ( (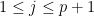 ), where the ), where the 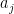 are unknown coefficients. Using the recurrence relation are unknown coefficients. Using the recurrence relation  , we obtain a linear combination of the monomials, which reduces to an easily solvable , we obtain a linear combination of the monomials, which reduces to an easily solvable 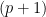 -by- -by-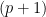 triangular linear system in the unknown coefficients triangular linear system in the unknown coefficients  of the closed-form polynomial solution. Maxima and Octave/Matlab codes for directly computing the closed-form solutions are included in the Appendices. of the closed-form polynomial solution. Maxima and Octave/Matlab codes for directly computing the closed-form solutions are included in the Appendices.
A lovely paper by Bearden (March 1996, American Mathematical Monthly), which was shared with me by a reader, tells the mathematical story nicely, with much of the history filled in.
Continue reading this article…
By Assad Ebrahim, on May 20th, 2010 (15,310 views) |
Topic: Maths--Tools, SWEng--Toolbox
(Mathematical Toolset Series: TeX & LaTeX, Part 3 of 3)
If you write frequently, it is likely that you have certain stock or administrative material that is included in each of your documents. You also likely spend a substantial portion of your overall effort re-writing, editing, or re-arranging material. In this situation, one of the best ways of preserving your time and your sanity is to adopt a modular approach to document development.
In this final article of the three part series on LaTeX / TeX, I will discuss a modular approach to document preparation using TeX. I’ll also provide modular templates that should make your use of TeX more efficient.
By Assad Ebrahim, on May 18th, 2010 (24,564 views) |
Topic: Maths--Tools, SWEng--Toolbox
Writing Beautiful Mathematics: Getting Started with LaTeX on Windows
If you haven’t done so already, you may want to start by reading the Preface to the Computing Series: Software as a Force Multiplier, Sections 1-3.
2nd ed. Revised with new templates Sep 21, 2019, 1st ed. May 18, 2010.
Getting Started with LaTex
LaTeX (open source, free) is an essential tool to write beautifully formatted mathematics efficiently. If you have extensive mathematical symbology and have been using MS Word for this, you are using the wrong tool for the job (see Figure below). Setting up LaTeX should take no more than an hour, after which you can produce publication-ready mathematical documents quickly and reliably. This article walks you through setting up a working platform for Windows, and provides the LaTeX templates you’ll need to produce your first examples. Also shared is the source code and compilation instructions for an example paper, which you can download and modify for your own use, containing several advanced stylistic elements (endnotes, figures with captions, URLs, code listings, and epigraphs).
 An example of mathematics written in LaTeX, from Finite Summation of Integer Powers (Part 3), A. Ebrahim, C. Ouellette, 2010. Continue reading this article…
…for Embedded and Low-Level Systems Development
C provides the convenience of learning one language while retaining the ability to target a variety of platforms including modern operating systems (Linux, Windows, Mac), real-time operating systems, systems-on-a-chip, and a host of microcontrollers for embedded development. And if you have to “mov” the bits around yourself (device drivers, DMA controllers), you can do that too. This is a significant efficiency over assembly languages which are essentially chip-specific control codes and therefore require understanding the architecture of the target chip.
Continue reading this article…
By Assad Ebrahim, on January 9th, 2010 (25,844 views) |
Topic: SWEng--Programming
2nd ed., Feb 1, 2024, 1st ed. Jan 9th, 2010
A common misconception is that assembly language programming is a relic of the past. This is certainly not the case, and assembly language remains a core knowledge area for embedded systems development, digital design, and algorithm development in the 21st century.
A second misconception, especially amongst those who are only familiar with higher level languages (Python, Ruby, C#/.NET, Perl), is that assembly language is a defective programming language and therefore not worth the time to invest in.
But assembly language is more than ‘just another general purpose programming language’. It is actually the control signal specification for the microprocessor or microcontroller that will be running the instructions, and whose digital design must be reasonably well understood in order to get it to work successfully.
Higher level languages typically hide the underlying toolchains behind turnkey integrated development environments (IDEs). But the toolchains are valuable in their own right, comprising various software components (pre-processor, compiler, assembler, linker, loader) which take the high level code and transform it to executable machine code that can run on the target processor, optionally producing assembly code for inspection along the way. Familiarity with this toolchain can help evaluate how much overhead the high-level tools introduce on the code, which is an important part of understanding how much you’re trading off.
In this article, we’ll look first take a look at the software toolchain involved in general terms, before turning to specific tools you can use on a modern Windows computer (through Windows 11) to target an x86 chip (no longer in your PC but in a DOS Emulator). Similar skills and approaches carry over to the toolchain for the Atmel 328P and ATTiny 85 with a graphics application (TinyPhoto) on the ATTiny85 here.
Continue reading this article…
|
Stats: 1,089,379 article views since 2010 (Aug '24 update)
Dear Readers: Welcome to the conversation! We publish long-form pieces as well as a curated collection of spotlighted articles covering a broader range of topics. Notifications for new long-form articles are through the feeds (you can join below). We love hearing from you. Feel free to leave your thoughts in comments, or use the contact information to reach us!
|


