Abstract This brief note explores the use of fuzzy classifiers, with membership functions chosen using a statistical heuristic (quantile statistics), to monitor time-series metrics. The time series can arise from environmental measurements, industrial process control data, or sensor system outputs. We demonstrate implementation using the R language on an example dataset (ozone levels in New York City). Click here to skip straight to the coded solution), or read on for the discussion.
 Fuzzy classification into 5 classes using p10 and p90 levels to achieve an 80-20 rule in the outermost classes and graded class membership in the inner three classes. Comparison with crisp classifier using the same 80-20 rule is shown in the bottom panel of the figure. Continue reading this article…
This article looks at Propositional Logic, also called Statement Calculus, from a combinatorial and algebraic point of view (Sections 3-6), its implementation in software (Section 7), and its application to digital electronics (Section 10). Historical sections cover the shift in viewpoint from classical logic based on Aristotle’s syllogism to modern symbolic logic (Section 2) and the axiomatization of logic (Section 9). (See logic sourcebook for the original source papers (1830-1881) that drove this shift.)
In Section 7, we implement the grammar of the statement calculus in the Symbolic Logic Simulator (SLS), a program written in 28 lines of Forth code, that allows computer-aided verification of any theorem in Propositional Logic (see Appendix 1 for source code). The program makes it straight-forward to explore non-obvious logical identities, and verify any propositional logic theorem or conjecture, in particular see Appendix 2 for key identities in the statement calculus (duality, algebraic, and canonical identities).
The concept of linguistic adequacy is developed in Section 8 and the NAND Adequacy Theorem is proved showing that NAND can generate all logical operations. A corollary is that any digital logic circuit can be built up entirely using NAND gates, illustrated using the free Digital Works software.
Continue reading this article…
In this article we look at the ideas of George Peacock whose 700-page opus A Treatise on Algebra (1830) transformed classical algebra into its modern form as an abstract symbolic science, free from the physical interpretation of quantity that had previously restricted it.
Continue reading this article…
By Assad Ebrahim, on January 21st, 2018 (52,762 views) |
Topic: Maths--Technical
2nd ed. January 21, 2018; 1st ed. Feb 8th, 2010
Abstract
This three part paper explores solving the sum of powers problem 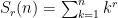 using discrete maths techniques (recurrence relations, matrix systems) to obtain a solution polynomials whose coefficients turn out to be exactly the Bernoulli numbers using discrete maths techniques (recurrence relations, matrix systems) to obtain a solution polynomials whose coefficients turn out to be exactly the Bernoulli numbers  . .
Part 1 (this paper) solves the problem using recurrence relations in a way which a high school student could emulate for small  . In Part 2, we develop a general recursive solution that works for arbitrary . In Part 2, we develop a general recursive solution that works for arbitrary  , from which we can build a table of values to assist in finding the coefficients of the solution polynomial, coefficients that are precisely the Bernoulli numbers discovered in 1713. In Part 3, we show how by transforming the problem into a linear system, we may obtain a direct (non-recursive) solution which directly calculates the Bernoulli number for any power , from which we can build a table of values to assist in finding the coefficients of the solution polynomial, coefficients that are precisely the Bernoulli numbers discovered in 1713. In Part 3, we show how by transforming the problem into a linear system, we may obtain a direct (non-recursive) solution which directly calculates the Bernoulli number for any power  . Source code is provided for all solutions. . Source code is provided for all solutions.
Readers who are interested in this topic are referred also to lovely paper by Bearden (March 1996, American Mathematical Monthly), which tells the mathematical story and fills in the history (thanks to a reader for this great reference).
Continue reading this article…
By Assad Ebrahim, on January 20th, 2018 (22,471 views) |
Topic: Maths--Technical
By Assad Ebrahim, on January 19th, 2018 (13,230 views) |
Topic: Mathematics, Maths--Technical
(Discrete Mathematics Techniques III)
1st ed. Apr 2nd, 2010
Abstract
This is the last in the 3-part series of articles on finding for oneself the solution to the sum of integer power problem, and in the process discovering the Bernoulli numbers. In Part 3 (this paper), we find a direct closed-form solution, i.e. one that does not require iteration, for the general case of the finite-summation-of-integer-powers problem 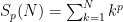 . Having established in Part 2 that the closed-form solution is a polynomial, the summation is here rewritten as the sum of the . Having established in Part 2 that the closed-form solution is a polynomial, the summation is here rewritten as the sum of the  independent monomials independent monomials 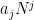 ( (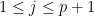 ), where the ), where the 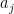 are unknown coefficients. Using the recurrence relation are unknown coefficients. Using the recurrence relation  , we obtain a linear combination of the monomials, which reduces to an easily solvable , we obtain a linear combination of the monomials, which reduces to an easily solvable 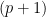 -by- -by-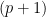 triangular linear system in the unknown coefficients triangular linear system in the unknown coefficients 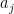 of the closed-form polynomial solution. Maxima and Octave/Matlab codes for directly computing the closed-form solutions are included in the Appendices. of the closed-form polynomial solution. Maxima and Octave/Matlab codes for directly computing the closed-form solutions are included in the Appendices.
A lovely paper by Bearden (March 1996, American Mathematical Monthly), which was shared with me by a reader, tells the mathematical story nicely, with much of the history filled in.
Continue reading this article…
By Assad Ebrahim, on February 25th, 2010 (52,593 views) |
Topic: Mathematics, Maths--Technical
Updated! February 5, 2017
The value of zero raised to the zero power, 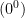 , has been discussed since the time of Euler in the 18th century (1700s). There are three reasonable choices: 1,0, or “indeterminate”. Despite consensus amongst mathematicians that the correct answer is one, computing platforms seem to have reached a variety of conclusions: Google, R, Octave, Ruby, and Microsoft Calculator choose 1; Hexelon Max and TI-36 calculator choose 0; and Maxima and Excel throw an error (indeterminate). In this article, I’ll explain why, for discrete mathematics, the correct answer cannot be anything other than 0^0=1, for reasons that go beyond consistency with the Binomial Theorem (Knuth’s argument). , has been discussed since the time of Euler in the 18th century (1700s). There are three reasonable choices: 1,0, or “indeterminate”. Despite consensus amongst mathematicians that the correct answer is one, computing platforms seem to have reached a variety of conclusions: Google, R, Octave, Ruby, and Microsoft Calculator choose 1; Hexelon Max and TI-36 calculator choose 0; and Maxima and Excel throw an error (indeterminate). In this article, I’ll explain why, for discrete mathematics, the correct answer cannot be anything other than 0^0=1, for reasons that go beyond consistency with the Binomial Theorem (Knuth’s argument).
Continue reading this article…
|
Stats: 1,089,379 article views since 2010 (Aug '24 update)
Dear Readers: Welcome to the conversation! We publish long-form pieces as well as a curated collection of spotlighted articles covering a broader range of topics. Notifications for new long-form articles are through the feeds (you can join below). We love hearing from you. Feel free to leave your thoughts in comments, or use the contact information to reach us!
|

