Sum of Integer Powers (Part 2)

By Assad Ebrahim, on January 20th, 2018 (21,796 views) | 4 comments - Leave a comment!
Topic: Maths--Technical

Spread the love

(Discrete Mathematics Techniques II)

1st ed. Feb 8th, 2010

Abstract
We continue the 3-part paper exploring how one might solve for themselves the general case of the sum-of-integer-powers problem $S_p(N) = \sum_{k=1}^{N} k^p$ for arbitrary $p$ , the coefficients of whose solution are the famous Bernoulli numbers (1716). In this paper we show to how obtain a $p$ -th order recurrence relation that can be used to iteratively obtain the closed form polynomial for $S_p(N)$ for any given $p$ . Source code is given for computing these polynomials using Maxima, an open-source (free) symbolic computation platform.

This article generalizes the recurrence relation approach that is motivated and illustrated for small $p$ in Part 1. A direct (non-recursive) method for computing the closed-form solutions is given in Part 3.

A lovely paper by Bearden (March 1996, American Mathematical Monthly), which was shared with me by a reader, tells the mathematical story nicely, with much of the history filled in.

NOTE: This paper contains many formulas. As such, you may prefer reading the paper as a typeset PDF.

Finding $S_p(N) = \sum_{k=1}^N k^p$

We desire a general formula that solves the finite-summation-of-integer-powers problem for any positive integer power $p$ :

$\displaystyle S_p(N) := \sum_{k=1}^N k^p, \mbox{ (where } p \in \mathbb{N} = \{0,1,2,\ldots\}; N\geq0). \ \ \ \ \ (1)$

We proceed using the method of recurrence relations that was illustrated for small $p$ in Part 1 of this paper [Ebr10] and that we prove inductively here.

Outline: We obtain a simple first-order recurrence relation (2) and a more complicated recurrence relation (5) that involves the coefficients of a lower order solution to (1). A sequence of manipulations followed by substitution of the first recurrence into the second yields the recurrence relation solution (10). Induction on $p$ shows that this is indeed the solution we seek, and that the closed form solution is a polynomial of degree $p+1$ with rational coefficients and no constant term. The recurrence relation (10) allows the closed form expressions to (1) to be computed iteratively for any $p$ . A direct (non-iterative) matrix method for computing the closed form solutions is given in Part 3 of this paper.

Deriving the Solution

Proceeding now to the solution:

Claim 1 The solution to (1) is a polynomial of degree $p+1$ with rational coefficients and no constant term.

In particular we shall find an expression (10) for this polynomial that allows a closed form for (1) to be computed iteratively for any given $p$ and all $N$ .

Proof: (By Induction)
Base case $p=0$ : the solution is immediate: $S_0(N) = \sum_{k=1}^N 1 = N$ . This is a polynomial of degree 1 with rational coefficients and no constant term.

For the inductive case, suppose the claim to be true for powers $1,2,\ldots,p-1$ . We shall show that it is then true for case $p$ .

Obtain the following recurrence directly from the problem statement (1):

$\displaystyle S_p(N) = S_p(N-1) + N^p.\ \ \ \ \ (2)$

This is a first recurrence.

Obtain a second recurrence from the problem statement (1) as follows: we have supposed in our induction hypothesis that the closed form solutions for the lower order problems are polynomials of a certain form. So we may write the $p-1$ solution as:

$\displaystyle S_{p-1}(N) = \alpha_p N^p + \sum_{j=1}^{p-1} \alpha_j N^j.\ \ \ \ (p\geq1; N\geq0) \ \ \ \ \ (3)$

In writing (3), the highest order term, $N^p$ , and its coefficient $\alpha_p$ , are emphasized.

Change variables in (3) from $N$ to $K$ , and solve for the highest order term $K^p$ :

$\displaystyle K^p = \frac{1}{\alpha_p}\left[S_{p-1}(K) - \sum_{j=1}^{p-1} \alpha_j K^j \right].\ \ \ \ \ (4)$

Substituting (4) into (1) gives the desired second recurrence, which we break into two summations for separate treatment:

$\displaystyle S_p(N) = \sum_{K=1}^N \frac{1}{\alpha_p} \left[S_{p-1}(K) - \sum_{j=1}^{p-1} \alpha_j K^j \right]$
$\displaystyle = \frac{1}{\alpha_p} \sum_{K=1}^N S_{p-1}(K) - \frac{1}{\alpha_p} \sum_{K=1}^N \sum_{j=1}^{p-1} \alpha_j K^j.\ \ \ \ \ (5)$

Considering each summation in (5) separately:

First summation in (5)…

Expand the first summation and gather the terms by like ( ${p-1}$ )-powers of $K$ :

$\displaystyle \sum_{k=1}^N S_{p-1}(K) = S_{p-1}(1) + S_{p-1}(2) + S_{p-1}(3) + \ldots + S_{p-1}(N)$
$\displaystyle \ \ \ \ \ = 1^{p-1} + (1^{p-1} + 2^{p-1}) + (1^{p-1} + 2^{p-1} + 3^{p-1}) + \ldots + (1^{p-1} + 2^{p-1} + 3^{p-1} + \ldots + N^{p-1})$
$\displaystyle \ \ \ \ \ = N(1^{p-1}) + (N-1)(2^{p-1}) + \ldots + 2(N-1)^{p-1} + 1(N^{p-1})$
$\displaystyle \ \ \ \ \ = \sum_{k=0}^{N-1} (N-K)(K+1)^{p-1}\ \ \ \ \ (6)$
Expand the binomial power in (6) using the binomial formula:
$\displaystyle \ \ \ \ \ = \sum_{k=0}^{N-1} (N-K)\sum_{j=0}^{p-1} \binom{p-1}{j} K^j$
$\displaystyle \ \ \ \ \ = \sum_{k=0}^{N-1} \sum_{j=0}^{p-1} (N-K)\binom{p-1}{j} K^j$
$\displaystyle \ \ \ \ \ = \sum_{k=0}^{N-1} \sum_{j=0}^{p-1} \binom{p-1}{j} \left[NK^j -K^{j+1}\right]$
Interchange the order of summation:
$\displaystyle \ \ \ \ \ = \sum_{j=0}^{p-1} \binom{p-1}{j} \sum_{k=0}^{N-1} \left[NK^j -K^{j+1}\right]$
Pull the $K=0$ term out of both summations. NOTE: $0^0 = 1$ ¹
$\displaystyle \ \ \ \ \ = N + \sum_{j=0}^{p-1} \binom{p-1}{j} \sum_{k=1}^{N-1} \left[NK^j -K^{j+1}\right]$
$\displaystyle \ \ \ \ \ = N + \sum_{j=0}^{p-1} \binom{p-1}{j} \left[\sum_{k=1}^{N-1} NK^j -\sum_{k=1}^{N-1}K^{j+1}\right]$
Recognize the appearance of the finite sum of integer powers, but of lower order:
$\displaystyle \ \ \ \ \ = N + \sum_{j=0}^{p-1} \binom{p-1}{j} NS_j(N-1) - \sum_{j=0}^{p-1} \binom{p-1}{j} S_{j+1}(N-1)$
Shifting indices in second summation, see [GKP] and [Knu]for index manipulation techniques:
$\displaystyle \ \ \ \ \ = N + \sum_{j=0}^{p-1} \binom{p-1}{j} N S_j(N-1) - \sum_{j=1}^{p} \binom{p-1}{j-1} S_j(N-1)$
Peel off $0$ -th term from first sum and $p$ -th term from second sum to combine the rest:
$\displaystyle \ \ \ \ \ = N + N(N-1) - S_p(N-1) + \sum_{j=1}^{p-1} S_j(N-1)\left[N\binom{p-1}{j} - \binom{p-1}{j-1}\right]$
$\displaystyle \ \ \ \ \ = N^2 - S_p(N-1) + \sum_{j=1}^{p-1} S_j(N-1)\left[N\binom{p-1}{j} - \binom{p-1}{j-1}\right]\ \ \ \ (7)$

Second summation in (5)…

The second summation term in (5) is a double summation. Recognize that the finite sum of $K^j$ summed over $K$ is in fact $S_j(N)$ . So interchange the order of summation and proceed:

$\sum_{k=1}^N \sum_{j=1}^{p-1} \alpha_j K^j = \sum_{j=1}^{p-1} \alpha_j \left(\sum_{k=1}^N k^j\right)$
$\displaystyle \ \ \ \ \ = \sum_{j=1}^{p-1} \alpha_j S_j(N).\ \ \ \ (8)$

Arriving at the final form of the second recurrence…

Combining (7) and (8) into the second recurrence (5) gives the simplified second recurrence:

$\displaystyle S_p(N) = \frac{1}{\alpha_p} \left\{N^2 - S_p(N-1) + \sum_{j=1}^{p-1} C_j(N)S_j(N-1) - \sum_{j=1}^{p-1} \alpha_j S_j(N) \right\}, \ \ \ \ \ (9)$

where

$\displaystyle C_j(N) = \left[\binom{p-1}{j} N - \binom{p-1}{j-1}\right]$

is a linear polynomial in $N$ with binomial coefficients.

Substituting $S_p(N-1)$ from the first recurrence (2) into (5) yields:

$\displaystyle S_p(N) = \frac{1}{\alpha_p} \left\{N^2 - S_p(N) + N^p + \sum_{j=1}^{p-1} C_j(N) S_j(N-1) - \sum_{j=1}^{p-1} \alpha_j S_j(N) \right\}.$

Collecting the $S_p(N)$ terms and simplifying gives a $p$ -th order recurrence relation that supplies a closed form expression for $S_p(N)$ in terms of lower order summations:

$\displaystyle S_p(N) = \frac{1}{1+\alpha_p}\left\{N^2 + N^p + \sum_{j=1}^{p-1} C_j(N) S_j(N-1) - \sum_{j=1}^{p-1} \alpha_j S_j(N) \right\}, \ \ \ \ \ (10)$

where the $\alpha_j$ are the coefficients from the closed form solution of $S_{p-1}(N)$ , and

$\displaystyle C_j = \left[N\binom{p-1}{j} - \binom{p-1}{j-1}\right].$

Inspection shows that the general solution (10) is a polynomial in $N$ that satisfies all three elements of Claim 1:

it has degree $p+1$ : $S_{p-1}(N-1)$ is a $p$ -th order polynomial multiplied by the linear polynomial $C_p-1(N)$ ,
it has no constant term
it has rational coefficients: the coefficients are sums and products of coefficients of lower order solutions (which are rational by the inductive hypothesis) and binomial coefficients (positive integers).

The Claim is therefore shown by induction.

Remarks We have in (10) a recurrence formula for the finite-summation-of-integer-powers problem that can be used to derive closed form expressions for any given $p$ .

Listing of Closed Form Solutions

Figure 1 shows the first 10 closed form expressions computed iteratively using Maxima. Maxima source code is provided in Appendix A.

Figure 1.

Figure 1. Closed form expressions for S_p(N), for p=1,2,...,10, computed using computer algebra system Maxima.

Conclusion

Summary We have developed a $p$ -th order recurrence relation (10) that, when used iteratively, gives the general closed form formula for the finite summation $\sum_{k=1}^N k^p$ for any given $p$ .

Computing closed form formulas for specific $p$ from this $p$ -th order recurrence is made substantially easier by a computer package, whether this is a symbolical algebra package such as Maxima, that gets through the tangle of algebra that arises out of what is effectively a chain of substitutions, or a programming language such as Ruby, that has flexible language structures allowing an iteration such as this to be coded up easily.

Appendix A provides Maxima source code that uses (10) to iteratively compute the closed form expression for $S_p(N)$ for any given $p$ .

Next Steps Can we do better? Specifically, can we find a closed form expression for solution that can be obtained directly, i.e. without requiring iteration? What relations hold between and among the $S_p(N)$ ? These matters are taken up in Part 3 of this paper [EO10]. In particular, Part 3 uses matrix methods to obtain the closed form expressions shown in Figure 1 directly and without requiring iteration, by solving a linear system.

Appendix A: Maxima Source Code for Computing 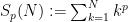$S_p(N) := \sum_{k=1}^N k^p$

This Appendix gives Maxima source code for computing closed form expressions for the finite-summation-of-integer-powers problem (1) using the $p$ -th order recurrence relation (10). Appendix B shows how both Maxima and Ruby can be used for cross-checking both the derivation and the correctness of the implementation.

The following Maxima code iteratively computes solutions for given values of p, using this $p$-th order recurrence relation.

Excerpt (Full Source):

/* **********************
CORE COMPUTATION: p-th ORDER RECURRENCE
—————————————
PRIVATE Function: Computes p-th solution using p-th order recurrence relation
of Equation (1-SOL), and prior solutions.
Solution in: “Finite Summation of Integer Powers, Part 2”, Assad Ebrahim, Jan 2010
Paper at: http://mathscitech.org/papers/ebrahim-sum-powers-2.pdf */
get_next_SpN(p) := block([a,sum1,sum2], s[0](n) := n, /* initial value */
c(p,j,n) := n*binomial(p-1,j) - binomial(p-1,j-1), /* definition */

a[p-1] : getcoeffs(s,p-1), /* get prior solution’s coefficients */

/* compute the two summations in Equation (1-SOL) */
sum1 : ratsimp(sum(c(p,k,n)*s[k](n-1),k,1,p-1)), sum2 : ratsimp(sum(a[p-1][k+1]*s[k](n),k,1,p-1)),
/* compute and assign solution (1-SOL) */
define(s[p](n),ratsimp((1/(1+a[p-1][p+1]))*(n^2 + n^p + sum1 - sum2))) )$

Download full Source Code here (or grab this file).

Appendix B: Using computing software to compute and check the derivation (10)

Cross-Checking Derivation of the General Formula Using Maxima and Ruby

We can check the derivation using computing software, as follows:

Use Maxima to obtain the simplified formula for $S_5(N)$ . (Figure 2)
Now, you could determine the $C_j(N)$ by hand, e.g.

$\displaystyle C_1 = \binom{4}{1}N - \binom{4}{0} = 4N-1$
$\displaystyle C_2 = \binom{4}{2}N - \binom{4}{1} = 6N-4$
$\displaystyle C_3 = \binom{4}{3}N - \binom{4}{2} = 4N-6$
$\displaystyle C_4 = \binom{4}{4}N - \binom{4}{3} = N-4,$

but why bother? Maxima has the facility to evaluate binomial coefficients, so just code up the general definition:

c(p,j,n):=n*binom(p-1,j) – binom(p-1,j-1);

$\displaystyle S_5(N) = \tfrac{1}{12}\left[2N^6 + 6N5 + 5N^4 - N^2\right]$
Use Maxima to evaluate this at, say, $N=10$ (Figure 3)
$\displaystyle S_5(10) = 220,825$
Use Ruby to perform the brute force summation $S_5(10) = \sum_{k=1}^{10} k^5$ (Figure 4). This yields the same value: 220,825.

Observe that the two computations of $S_5(10)$ match. One can check at various values of $N$ and convince oneself that the derivation is correct. Note: Being convinced of the correctness of a derivation through computing values is not the same thing as a proof of correctness. It is, however, important to catch errors, both typographical and in implementation.

Figure 2.

Figure 2. Obtaining closed form for S_5(N) using Symbolic Simplification in Maxima

Figure 3.

Figure 3. Evaluation of S_5(10) in Maxima

Figure 4.

Figure 4. Brute force summation S_5(10) in Ruby (irb)

Appendix C: Why 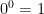$0^0 =1$

A key step in the derivation of (7) from (6) relies on the fact that $0^0 = 1$ . Recall, we peeled off the $K=0$ term of the inner summation to get: $N0^j - 0^{j+1}$ . Peeling this out of the outer summation requires considering the expression for all $j$ . Now, 0 raised to any positive power is 0, so we can dispel the case of $j>0$ . But what is $0^0$ ? A decision must be made: it is either $0$ or $1$ . Indeterminacy is not an options, since the situation is real and is required to continue the simplification.

This question is treated here: Why $0^0 =1$

Acknowledgements

I thank Carol Ouellette for reading an early draft of this paper and for many thoughtful comments and suggestions.

>> Continue reading: Finite Summations of Integer Powers $x^p$ , Part 3

This article is available for download as a PDF here.

The Maxima source code implementing the recurrence relation solution is available for download here.

References

[Ebr10]

Finite summation of integer powers x^p, part 1.
Assad Ebrahim.
February 2010.

[EO10]

Finite summation of integer powers x^p, part 3.
Assad Ebrahim and Carol Ouellette.
April 2010.

[GKP]

Concrete Mathematics: A Foundation for Computer Science.
Ron Graham, Donald Knuth, and Oren Patashnik.
1994, 2nd edition.
Addison Wesley.

[Knu]

The Art of Computer Programming (3 Volumes).
Donald Knuth.
Addison Wesley.
1968, 1969, 1973 (Latest boxed edition of 2011 includes Vol4A)

Footnotes

Peel off the $K=0$ term of the inner summation to get: $N0^j - 0^{j+1}$ . Peeling this out of the outer summation requires considering the value of the expression when summed over all values of $j$ . Now, 0 raised to any positive power is 0, so we can dispel the case $j>0$ . This leaves:
$\displaystyle \binom{p-1}{0}\left(N0^0 - 0^1\right)$

What is $0^0$ ? A decision must be made: it is either $0$ or $1$ . Indeterminacy is not an option, since the situation is real and is required to continue the simplification. This step in the derivation of (7) from (6) relies on the empirical fact that $0^0 = 1$ .

Definition 1 (Empirical) $0^0 = 1$ for $k^j$ , where $k,j$ are discrete variables.

(The empirical basis for this definition is discussed in Appendix C.) With this definition, the value of the $K=0$ term summed over all values of $j$ is $N$ , and we proceed with the simplification toward (7). ↩

Michael

July 31, 2019 at 16:15

Would like to share my blog on power summation at :

https://vroomlab.wordpress.com/2017/07/19/little-bird-and-a-recursive-generator/

The algorithm is derived geometrically. it is also implemented in Maxima.

Assad Ebrahim

August 2, 2019 at 03:12

@Michael – nice derivation, thanks for sharing.

Alise Alsopp

December 18, 2019 at 16:52

thanks! your paper can really help me a lot

Seven fields of Computer Programming: A survey from 1940s to the present « Mathematical Science & Technologies

February 10, 2020 at 02:41

[…] from this site are: Finite Summations of Integers (1-Mathematical, 2-Maxima, 3-Octave), Maxima for Symbolic Computation, Mathematics of Duelling (R […]

Mathematical Science & Technologies