Electronics, computing, and applied mathematics are gateway subjects to modern technology.
For young learners, we believe that electronics provides an ideal entry point. It is practical, with manipulables. It is easy to see cause and effect. With the right equipment and approach, exploring electronics can begin for children as early as 3 years old.
There are many tangible benefits for young learners getting started in electronics:
- fine motor skill development,
- an intuition for how technological things work at a component level,
- the integration of technology into the palette for imagination and creativity,
- improved self-confidence,
- strengthening a growth mindset,
- building resilience,
- raising the threshold of frustration,
- better dexterity,
- stronger focus.
 A three year old wiring his first circuit and the joy at seeing the LED, which he selected, light up! Continue reading this article…
By Assad Ebrahim, on January 21st, 2018 (52,649 views) |
Topic: Maths--Technical
2nd ed. January 21, 2018; 1st ed. Feb 8th, 2010
Abstract
This three part paper explores solving the sum of powers problem 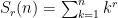 using discrete maths techniques (recurrence relations, matrix systems) to obtain a solution polynomials whose coefficients turn out to be exactly the Bernoulli numbers using discrete maths techniques (recurrence relations, matrix systems) to obtain a solution polynomials whose coefficients turn out to be exactly the Bernoulli numbers  . .
Part 1 (this paper) solves the problem using recurrence relations in a way which a high school student could emulate for small  . In Part 2, we develop a general recursive solution that works for arbitrary . In Part 2, we develop a general recursive solution that works for arbitrary  , from which we can build a table of values to assist in finding the coefficients of the solution polynomial, coefficients that are precisely the Bernoulli numbers discovered in 1713. In Part 3, we show how by transforming the problem into a linear system, we may obtain a direct (non-recursive) solution which directly calculates the Bernoulli number for any power , from which we can build a table of values to assist in finding the coefficients of the solution polynomial, coefficients that are precisely the Bernoulli numbers discovered in 1713. In Part 3, we show how by transforming the problem into a linear system, we may obtain a direct (non-recursive) solution which directly calculates the Bernoulli number for any power  . Source code is provided for all solutions. . Source code is provided for all solutions.
Readers who are interested in this topic are referred also to lovely paper by Bearden (March 1996, American Mathematical Monthly), which tells the mathematical story and fills in the history (thanks to a reader for this great reference).
Continue reading this article…
By Assad Ebrahim, on January 20th, 2018 (22,331 views) |
Topic: Maths--Technical
By Assad Ebrahim, on January 19th, 2018 (13,151 views) |
Topic: Mathematics, Maths--Technical
(Discrete Mathematics Techniques III)
1st ed. Apr 2nd, 2010
Abstract
This is the last in the 3-part series of articles on finding for oneself the solution to the sum of integer power problem, and in the process discovering the Bernoulli numbers. In Part 3 (this paper), we find a direct closed-form solution, i.e. one that does not require iteration, for the general case of the finite-summation-of-integer-powers problem 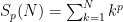 . Having established in Part 2 that the closed-form solution is a polynomial, the summation is here rewritten as the sum of the . Having established in Part 2 that the closed-form solution is a polynomial, the summation is here rewritten as the sum of the  independent monomials independent monomials  ( (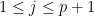 ), where the ), where the 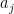 are unknown coefficients. Using the recurrence relation are unknown coefficients. Using the recurrence relation  , we obtain a linear combination of the monomials, which reduces to an easily solvable , we obtain a linear combination of the monomials, which reduces to an easily solvable 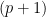 -by- -by-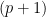 triangular linear system in the unknown coefficients triangular linear system in the unknown coefficients 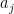 of the closed-form polynomial solution. Maxima and Octave/Matlab codes for directly computing the closed-form solutions are included in the Appendices. of the closed-form polynomial solution. Maxima and Octave/Matlab codes for directly computing the closed-form solutions are included in the Appendices.
A lovely paper by Bearden (March 1996, American Mathematical Monthly), which was shared with me by a reader, tells the mathematical story nicely, with much of the history filled in.
Continue reading this article…
*New!* (29 Aug 2020) – Turtle Logo v1.8 (portable) is available! Developer kit with source code included. Suitable from ages 3 years to adult. (970 lines of Forth code).
1. Inspiring the next generation of technology builders.
A challenge facing parents and teachers is how to help children develop ‘builder’ relationships with technology rather than being limited to the passive consumption of content created by others. The consensus on what’s important for older kids and adults is clear: coding. This enables children to participate in the creation of their own technological “micro-worlds” — environments rich in educational potential.[14]
This autumn, spurred by having our own young children (one aged 4 years, the other 16 months), we began an experiment, the result of which is a Turtle Logo program for Windows computers (freely downloadable) that is simple enough to be accessible for children from 3 years and older, while providing an extensible platform that can grow with the child.
The long-term goal is to enable children to express their creativity, artistry, and natural ‘builder’ impulses using coding, computer graphics, and robotics as readily as the previous generation could using paints, brushes, and building blocks.
 Turtle Logo – Inspiring the next generation of technology builders. Continue reading this article…
By Assad Ebrahim, on July 13th, 2016 (10,851 views) |
Topic: Education
Thoughts on Teaching Mathematics in an Exploratory, Dialectical, Topical format.
(2nd ed. July 13th 2016; 1st ed. Jan 31, 2010)
Mathematics is a richly spun tapestry, threaded with interconnections from a multiplicity of endeavors, perspectives, and disciplines, both theoretical and applied. Yet contrary to this “non-linear” reality, the typical pattern of school and even university mathematics is both linear and restricted.
This article takes a look at what lies behind the way things are, and what could bring positive change.
Continue reading this article…
By Assad Ebrahim, on October 18th, 2015 (5,295 views) |
Topic:
Below a quick reference for various useful code snippets…
- Forth
- LaTeX
- HTML
Forth snippets
Forth has many dialects. I use GForth for general purpose Forth, as it is available for both Linux and Windows (including Win8) and has a floating point stack which is convenient for scientific programming. I use Win32Forth for its Win32 facilities and easy integration with assembly language. I use F-PC for its simple design and compatibility with 16-bit i-x86 assembly language, though it needs to run in a 16-bit emulator such as DosBox.
Floating Point
\ extra stack operations
: f2dup ( fa fb -- fa fb fa fb ) fover fover ;
: funder ( fa fb -- fb fa fb ) fswap fover ;
\ useful scaffolding within loops
: fshowstack ( -- ) cr f.s key drop ;
: fshowtop ( -- ) cr fdup f. ;
\ float ops
: f2* ( fa -- 2fa ) fdup f+ ;
: f^2 ( fa -- fa^2 ) fdup f* ;
\ float equality
: feps 1e-12 ; \ proxy for machine epsilon
: f=eps ( fa fb -- bool ) f- fabs feps f< ; \ true if fa and fb within neighborhood of feps
LaTeX snippets
Packages
\usepackage{amsfonts} allows $\mathbb{R}$ for reals, $\mathbb{Z}$ for integers, $\mathbb{R}^n$ for n-dim. spaces.
\usepackage{amsmath} gives \eqref, \binom, \eqrefm, and more
\usepackage{amssymb} gives full AMS mathematics symbology
-
\usepackage{graphicx} allows incorporating images. EPS format is required though; png2eps is a useful conversion utility.
graphicx Reference
Example: \includegraphics[scale=0.4]{file}
-
\usepackage[pass]{geometry} allows changing margins within the document
Whitespace and Margins
\newgeometry{top=2.5cm,bottom=2.3cm,left=2.5cm,right=2.3cm}
What is the right text block size for comfortable reading? Conventional guidance is 60 characters per line, 80 characters upper limit. Yet 90-100 characters is comfortable for technical material. The 'right' number probably depends on content type (fiction, news, technical, mathematics) and reader experience. For example, experienced mathematicians either skim headings, formulas, theorems, figures or carefully read every word in a subsection of interest. In the first case, having more on the page (vertical compression) is a benefit: fewer pages to turn, easier to refer to previous statements. In the second case, the reading is deliberate enough that slightly longer lines don't matter; they are not long enough to cause 'doubling' (accidentally reading the same line twice).
Text Format
Verbatim / Code Formatting
\texttt{sqrt} for verbatim style on a phrase
- for verbatim code block, using a smaller font size:
{\footnotesize\begin{verbatim}
: f2dup ( fa fb -- fa fb fa fb ) fover fover ;
: funder ( fa fb -- fb fa fb ) fswap fover ;
\end{verbatim}
}
Referring to Labelled / Numbered blocks
\begin{lemma} your lemma name here \label{theorem_trivial}\end{lemma}
your lemma text here sets label
-
\ref{theorem_trivial} refers to named label internal numbering.
-
\pageref{theorem_trivial} refers to named label page number.
- Note run LaTeX twice to get refs correct.
-
\begin{equation} formula_text \label{labelname}\end{equation} numbers equations and sets reference.
- Equation
\eqref{labelname} refers to labelled equation's number
Equations
- Text inside math equations:
$\epsilon_{\text{machine}}$
- Numbered equations:
\begin{equation} formula_text \label{labelname}\end{equation} numbers equations and sets reference.
- Multi-line numbered equations :
\begin{align} line 1 ... \\
line 2 ... \end{align}
- use
\nonumber to suppress line numbers
- end a line with
\\
- use
align* to suppress all line numbers
- use
& to align at a character
- Cases:
\begin{equation}
x_{ij} =
\begin{cases}
0& \text{if $i \neq j$},\\
1& \text{if i=j}.
\end{cases}
\end{equation}
- Stacked Text, e.g. for limits
\lim{x \to 2} or usepackage{mathtools} and then \substack{first line\\second line\\third line}
Figures and Captions
- Utility for converting PNG to EPS (zip)
- Captioning a figure Reference
Caption is placed in the same position before/after graphic
\begin{figure}[h!]
\includegraphics[scale=0.3]{sqrt_xls_2} % Excel hand calc
\caption{Variation suitable for hand calculation.}
\label{fig:sqrt_xls_2_hand}
\end{figure}
- Referring to labelled figure label reference
Figure \ref{sqrt_xls_2_hand}
- Text wrapping a figure (wraps the text below it)
\begin{wrapfigure}{R}{0.75\textwidth}
\centering
\includegraphics[width=0.75\textwidth]{sqrt_xls_1_sqrt2}
\caption{\label{fig:sqrt2} Calculate $\sqrt{2}$}
\end{wrapfigure}
Useful Macro Commands
- Already defined: \lim, \sin, \min, \arctan, \to, etc.
- For analysis
\newcommand{\dt}{\ensuremath{\text{d}t}} % for calculus dt symbol
\newcommand{\diff}[1]{\ensuremath{\text{d#1}}} % for calculus dx, dy, dz, dt differential
\newcommand{\qed}{\ensuremath{\ \ \blacksquare}} %for end of proof symbol
\newcommand{\qedlt}{\ensuremath{\ \ \square}} %for end of proof symbol
\newcommand{\eps}{\ensuremath{\epsilon}} %for easy use of epsilon
\newcommand{\imply}{\rightarrow} % for => % Longrightarrow, etc.
\newcommand{\limply}{\leftarrow} % for =>
\newcommand{\bimply}{\leftrightarrow} % for <=>
\newcommand{\st}{\ensuremath{\ \ \text{s.t.}\ \ }} % for easy use of s.t. (such that) in a formula
\newcommand{\inv}{\ensuremath{^{-1}}} % for easy creation of f^{-1}, etc.
- For logic and set theory
% MACRO for nice emptyset
\let\oldemptyset\emptyset
\let\emptyset\varnothing
\newcommand{\dcup}{\ensuremath{\ \ \dot\cup \ \ }} % for disjoint union
% \setminus instead of \backslash
% TEXT words for logical operators
\newcommand{\AND}{\ensuremath{\text{\begin{ttfamily}\small{ AND }\end{ttfamily}}}}
\newcommand{\OR}{\ensuremath{\text{\begin{ttfamily}\small{ OR }\end{ttfamily}}}}
\newcommand{\NOT}{\ensuremath{\text{\begin{ttfamily}\small{ NOT }\end{ttfamily}}}}
\newcommand{\XOR}{\ensuremath{\text{\begin{ttfamily}\small{ XOR }\end{ttfamily}}}}
\newcommand{\NAND}{\ensuremath{\text{\begin{ttfamily}\small{ NAND }\end{ttfamily}}}}
\newcommand{\NOR}{\ensuremath{\text{\begin{ttfamily}\small{ NOR }\end{ttfamily}}}}
\newcommand{\XNOR}{\ensuremath{\text{\begin{ttfamily}\small{ XNOR }\end{ttfamily}}}}
\newcommand{\TRUE}{\ensuremath{\text{\begin{ttfamily}\small{ TRUE }\end{ttfamily}}}}
\newcommand{\FALSE}{\ensuremath{\text{\begin{ttfamily}\small{ FALSE }\end{ttfamily}}}}
\renewcommand{\neg}{\sim} % symbolic not defined now to use tilde ~ instead of ¬
\newcommand{\eqdef}{\ensuremath{=_\text{\tiny def}}} % decorating = with `by definition'
- For variable decoration
\let\oldforall\forall % old takes the former command
\renewcommand{\forall}{\ \ \oldforall} % adds space before a logical operator
\let\oldexists\exists % old takes the former command
\renewcommand{\exists}{\ \ \oldexists} % adds space before a logical operator
\renewcommand{\vec}[1]{\mathbf{#1}} % vectors are bold
\newcommand{\pder}[2]{\frac{\partial#1}{\partial#2}} % for partial derivatives
\let\oldhat\hat % oldhat takes on what hat formerly had
\renewcommand{\hat}[1]{\oldhat{\mathbf{#1}}} % hats make vectors bold and hatted vectors
\newcommand{\overbar}[1]{\ensuremath{\overline{#1}}} % defines \overbar, which is more prominent than \bar and more convenient than overline
\newcommand{\fuzzy}[1]{\ensuremath{ \underset{\sim}{#1} }} % usage: \fuzzy{A} for A under-tilde
% \newcommand{\minimise}[1]{\ensuremath{\underset{#1}\min}} % usage: \minimise{x} for min over x NOT NEEDED \min_{ } already does this...
\newcommand{\set}[1]{\ensuremath{ \{#1\}}} % usage: \set{x_i}_{i=1}^N
- For tildes
\newcommand{\overtilde}[1]{\ensuremath{ \overset{\sim}{#1} }} % usage: \tilde{x} for x over-tilde
% \newcommand{\approx}{\ensuremath{\sim}} % usage: \approx 3
\newcommand{\abs}{\ensuremath{\text{abs}}} %for absolute value
- For probability AND statistics
\newcommand{\pr}[1]{\ensuremath{\text{Pr}\{#1\}}} %for probability, e.g. Pr(X=k)
\newcommand{\e}[1]{\ensuremath{\text{E}[#1]}} % expectation
\newcommand{\var}[1]{\ensuremath{\text{var}[#1]}} %for variance
\newcommand{\avg}{\ensuremath{\text{avg}}} %for avg
\newcommand{\sd}{\ensuremath{\text{sd}}} %for standard deviation
\newcommand{\cov}[2]{\ensuremath{\text{cov}(#1,#2)}} %for covariance
\newcommand{\cor}[2]{\ensuremath{\text{cor}(#1,#2)}} %for correlation
- For COMBINATORICS AND DISCRETE MATHS
\let \oldbinom\binom
\renewcommand{\binom}[2]{C\oldbinom{#1}{#2}} %This adds a C(a;b) to the choose notation
\newcommand{\floor}[1]{\ensuremath{\left\lfloor#1\right\rfloor}} %for floor and ceiling
\newcommand{\ceil}[1]{\ensuremath{\left\lceil#1\right\rceil}}
\newcommand{\lcm}{\ensuremath{\mbox{lcm} }} % LCM -- because \gcd is defined
\newcommand{\falling}[1]{\ensuremath{\underline{#1}}} % For use with falling factorial, and N-lower k, etc.
- For Physics
\newcommand{\micro}{\ensuremath{\mu}} %for micro symbol, e.g. uPa (micro-Pascals)
\newcommand{\dB}{\ensuremath{\text{ dB }}} %for dB
\newcommand{\kHz}{\ensuremath{\text{ kHz }}} %for kHz
\newcommand{\Hz}{\ensuremath{\text{ Hz }}} %for Hz
\renewcommand{\deg}{\ensuremath{^\circ}} %for circle degree symbol \deg uses a text style word and not a math style 15\deg C
- For Convenience
%MACRO FOR: \BEGIN{EQUATION} FORMULA_TEXT \END{EQUATION} numbered equation
\newcommand{\be}{\begin{equation}}
\newcommand{\ee}{\end{equation}}
- For BUSINESS (copyrights, trademarks, etc.) Reference
\def\registered{\ooalign{\hfil\raise .00ex\hbox{\scriptsize R}\hfil\crcr\mathhexbox20D}}
% usage: $^\registered$
% suggested by: Scott D. Anderson, anderson@cs.umass.edu
\def\tm{\leavevmode\hbox{$\rm {}^{TM}$}}
% usage: \tm
% suggested by: Patrick TJ McPhee Toronto Canada ptjm@io.org
HTML snippets
- Images, resized
(in angle brackets) img src="http://mathscitech.org/.../mjoy-demo.png" alt="example" style="width:367px;height:385px;"
By Assad Ebrahim, on November 11th, 2014 (410 views) |
Topic: Maths--General Interest
Updated: 2014-11-23
MetaMoji Note: A worthy digital replacement to Pencil & Notebook for creating freehand diagrams on Windows and Android.
Pencil & Notebook are hard to beat when diagrams, equations, and words are desired in roughly equal measure, which is common when working as an engineer, mathematician, or product designer. To be sure, there are good digital tools for subsets of these (example LaTeX), but not when all three are combined. But now there’s a new suite of digital freehand tools that are almost good enough to set aside the notebook and pencil permanently. The core of this toolkit is a vector-based graphics canvas (software) and an ultra-precise stylus (hardware).
If you use Apple iOS, you may already be using Adobe Ideas, which does the job brilliantly and is free (see this excellent article by Simon Raper). [1] But Adobe has no plans to release this to either Windows RT or Android, so for the rest of us, that’s a show-stopper, until now, with MetaMoji…
Continue reading this article…
By Assad Ebrahim, on May 21st, 2014 (7,898 views) |
Topic: Maths--General Interest
Duelling with pistols. If you were the one issuing the challenge, your dilemma was that custom dictated that your adversary be allowed to shoot first. Only then, if you were still able to shoot, would you be permitted to seek “satisfaction”.
How much of an advantage does the first shooter really have? In this article, we build a simple probability model, and implement a numerical model in a few lines of R code.
 Two gentleman face off in the snow. Convention dictates the challenged shoots first. Continue reading this article…
THIS PAGE HAS MOVED!
The essay has been incorporated into the Software list. You can find it here!
|
Stats: 1,089,379 article views since 2010 (Aug '24 update)
Dear Readers: Welcome to the conversation! We publish long-form pieces as well as a curated collection of spotlighted articles covering a broader range of topics. Notifications for new long-form articles are through the feeds (you can join below). We love hearing from you. Feel free to leave your thoughts in comments, or use the contact information to reach us!
|




