By Assad Ebrahim, on March 14th, 2010 (14,744 views) |
Topic: Maths--General Interest
Data Science & Advanced Analytics
19-21.Oct.2015 (Paris, France)
2015 IEEE International Conference on Data Science & Advanced Analytics (DSAA) will consist of two main tracks, Research and Applications. The Research Track is aimed at collecting contributions related to theoretical foundations of Data Science and Data Analytics. The Applications Track is aimed at collecting contributions related to applications of Data Science and Data Analytics in real life scenarios.
Digital & Web Analytics | Predictive Analytics | Big Data Summits
14-15.May.2014 (London, UK)
At the Bishopsgate Conference Centre in London for this year’s Analytics Innovation Summit.
Booking.com: Data Science
6.Dec.2013 (Amsterdam, Netherlands)
At Booking.com’s head office in Amsterdam, one of the leading players in the eTravel space. The Booking team has a raft of interesting problems in front of them, a bunch of smart, capable data scientists, and a real appetite for applying statistical / machine learning techniques to unlock the next level of benefits. A refreshing visit!
Silicon Milkroundabout 6.0: Analytics
16.Nov, 2013 (London, UK)
At Silicon Milkroundabout 6.0 this weekend. Key question: To what extent are predictive analytics technologies at the heart of the next generation of startups?
(Location: The Old Truman Brewery, 81 Brick Lane, London E1 6QL)
Update:
There are several promising startups in UK’s East End (Silicon Valley lite). The interesting ones (to my mind) were in retail analytics, peer-to-peer lending, even a novel education startup attempting to exploit machine learning techniques. Although the recruitment atmosphere detracts somewhat, SMR is a useful way to assess the next batch of promising start-ups.
Five outstanding startups were:
Predictive Analytics World Conference
23-24.Oct, 2013 (London, UK)
At the Predictive Analytics World Conference for at least part of the Conference, schedule permitting. The programme can be found here: PAW 2013 Programme
Advanced Analytics | Big Data | Hadoop | Social Media | Digital Innovation
30.Apr-1.May, 2013 (London, UK)
At the Advanced Analytics Innovation Summit. This year’s summits are being held at the Lancaster London Hotel, London, UK. (PDF Programme)
(Online Programmes)
Advanced Analytics | Big Data | Hadoop | Social Media | Digital Innovation
Crowd-Source Analytics & Entrepreneurship
9.Mar.2013 (London, UK)
At London Business School discussing the application of advanced data discovery algorithms for a new venture crowd-sourcing business concept.
SAP F&R User Conference
18-19.Sep,2012 (Dresden, Germany)
At the SAP Forecasting & Replenishment User Conference in Dresden, Germany, at the Maritim Hotel & International Congress Centre. This Conference is well attended by senior technical staff from SAF (Simulation, Analysis, and Forecasting) group, which has now become SAP’s Centre of Excellence based out of Schweiz, Switzerland after being acquired by SAP in 2009/2010.
Predictive Analytics & Big Data Innovation Summit
18-19.Apr, 2012 (London, UK)
At the Predictive Analytics & Big Data Innovation Summit. This year, the summit is being held at the Victoria Park Plaza Hotel, London, UK.
Predictive Analytics Innovation Summit
2.Jun & 3.Jun, 2011 (London, UK)
At the Predictive Analytics Innovation Summit (Jumeirah Carlton Towers, Knightsbridge, London, UK).
Third Aladdin (Autonomous Learning Agents for Decentralised Data and Information Networks) Symposium
27.Sep.2010 (Farnborough, UK)
At the Third Aladdin Symposium on Autonomous Learning Agents for Decentralised Data and Information Networks (BAE Systems, Park Centre, Farnborough, UK).
Unmanned Underwater Vehicles Showcase (UUVS) 2010
21-22.Sep.2010 (Southampton, UK)
At the Unmanned Underwater Vehicles Showcase (UUVS) 2010 (National Oceanography Centre, Southampton, UK).
Oceanology International 2010
9-11.Mar.2010 (London, UK)
At Oceanology International 2010 (EXCEL Centre, London, UK).
Advisory Committee on Mathematics Education
2.Mar.2010 (London, UK)
At the ACME Conference 2010 (Royal Society, London, UK).
Articles Repository Online
29.Dec.2009
The Articles Repository for Mathematical Science & Technologies is now online.
By Assad Ebrahim, on March 5th, 2010 (16,721 views) |
Topic: Technology
“Smart dust”, tiny leaf sensors, wearable computing — these and a host of other sensors that make measurements and communicate without requiring human intervention can now be readily integrated into dispersed systems to provide ambient intelligence, situational awareness, and the capability for adaptive behaviors or intelligent process automation.
Whether the sensor’s output is used to control the opening and closing of relays or thermostats, or to automatically raise alerts — the integration of sensors into systems is at the heart of the promise of ubiquitous computing. With the ability to place hundreds of embedded sensors within a given coverage area, each wirelessly streaming information, the possibility of self-organizing sensor networks is increasingly becoming a reality.
This article takes a look at the sensor layer of a basic ubiquitous computing stack.
Continue reading this article…
By Assad Ebrahim, on February 25th, 2010 (50,082 views) |
Topic: Mathematics, Maths--TechnicalUpdated! February 5, 2017
The value of zero raised to the zero power, 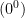 , has been discussed since the time of Euler in the 18th century (1700s). There are three reasonable choices: 1,0, or “indeterminate”. Despite consensus amongst mathematicians that the correct answer is one, computing platforms seem to have reached a variety of conclusions: Google, R, Octave, Ruby, and Microsoft Calculator choose 1; Hexelon Max and TI-36 calculator choose 0; and Maxima and Excel throw an error (indeterminate). In this article, I’ll explain why, for discrete mathematics, the correct answer cannot be anything other than 0^0=1, for reasons that go beyond consistency with the Binomial Theorem (Knuth’s argument).
Continue reading this article…
By Assad Ebrahim, on February 22nd, 2010 (63,794 views) |
Topic: Maths--Tools
If you haven’t done so already, you may want to start by reading the Preface to the Computing Series: Software as a Force Multiplier, Sections 1-3.
Maxima: a Computer Algebra System (CAS) for symbolic computation
Last updated: Feb 19, 2023 (fixed links). Nov 11, 2022 (added omega-math’s excellent web interface, and generating function calculation of the partition of integers problem).
Maxima is a computer algebra system (CAS) for symbolic computation that is free, open source, runs on multiple operating systems (Win,Mac,Linux), and covers a wide range of mathematical capabilities and graphical capabilities. These include algebraic simplification, polynomials, methods from calculus, matrix equations, differential equations, number theory, combinatorics, hypergeometric functions, tensors, gravitational physics, PDEs, nonlinear systems, plus including 2-D/3-D plotting and animation. With a large and responsive user community, there is plenty of help to get up the learning curve, and with its active developer base, Maxima and its ecosystem continue to gain capability, including a fantastic web interface by Omega-Math/Vroom-Labs (see the screenshot below, r0*0). The result is a free, versatile, powerful mathematical computing package for engineers, scientists, mathematicians, programmers, and students. This article will help you get started with Maxima and set you up with resources to flatten the learning curve.
 Omega-Math’s web interface to Maxima. Used here to calculate the first 10 elements of p(n), the number of ways to partition integer n, using a generating function comprising a truncated series of polynomials up to degree n=10
…for Embedded and Low-Level Systems Development
C provides the convenience of learning one language while retaining the ability to target a variety of platforms including modern operating systems (Linux, Windows, Mac), real-time operating systems, systems-on-a-chip, and a host of microcontrollers for embedded development. And if you have to “mov” the bits around yourself (device drivers, DMA controllers), you can do that too. This is a significant efficiency over assembly languages which are essentially chip-specific control codes and therefore require understanding the architecture of the target chip.
Continue reading this article…
By Assad Ebrahim, on January 31st, 2010 (8,422 views) |
Topic: Education, Maths--Philosophy
The mathematician Alfred North Whitehead observed that “[Advancement occurs] by extending the number of important operations which we can perform without thinking of them.” (Introduction to Mathematics, 1911 ) This is certainly true in mathematics where the development of judicious notation, accompanied by good mathematical technique, extends the capability to perform chains of complex reasoning accurately and efficiently. Through proper problem formulation (tractable yet generalizable), one can sometimes pass from a single insight to the solution of a family of problems, and in some cases, to the solution to the general question itself.
Here, mathematical computing can provide a useful benefit: helping to efficiently explore conjectures, dispatch with false directions, and save time during the development, error-checking and validation stages of obtaining general results. In industry, where specific or semi-general results are needed fast, such tools allow rapidly working up the required material and providing the necessary certainty before the fully general results or complete proof are ready.
Continue reading this article…
By Assad Ebrahim, on January 15th, 2010 (13,416 views) |
Topic: Maths--History, Maths--Philosophy
The development of mathematics has had many encouraging forces: societal, technological, cultural. These have served to accelerate mathematics and have been accelerated in turn, in many cases the pair becoming locked into a mutually beneficial resonance that has dramatically energized both.
In this article, I look at some of the significant catalysts, from the rise of the leisured class in ancient times to the impact of computing in modern times.
Continue reading this article…
By Assad Ebrahim, on January 9th, 2010 (21,379 views) |
Topic: SWEng--Programming
2nd ed., Feb 1, 2024, 1st ed. Jan 9th, 2010
A common misconception is that assembly language programming is a relic of the past. This is certainly not the case, and assembly language remains a core knowledge area for embedded systems development, digital design, and algorithm development in the 21st century.
A second misconception, especially amongst those who are only familiar with higher level languages (Python, Ruby, C#/.NET, Perl), is that assembly language is a defective programming language and therefore not worth the time to invest in.
But assembly language is more than ‘just another general purpose programming language’. It is actually the control signal specification for the microprocessor or microcontroller that will be running the instructions, and whose digital design must be reasonably well understood in order to get it to work successfully.
Higher level languages typically hide the underlying toolchains behind turnkey integrated development environments (IDEs). But the toolchains are valuable in their own right, comprising various software components (pre-processor, compiler, assembler, linker, loader) which take the high level code and transform it to executable machine code that can run on the target processor, optionally producing assembly code for inspection along the way. Familiarity with this toolchain can help evaluate how much overhead the high-level tools introduce on the code, which is an important part of understanding how much you’re trading off.
In this article, we’ll look first take a look at the software toolchain involved in general terms, before turning to specific tools you can use on a modern Windows computer (through Windows 11) to target an x86 chip (no longer in your PC but in a DOS Emulator). Similar skills and approaches carry over to the toolchain for the Atmel 328P and ATTiny 85 with a graphics application (TinyPhoto) on the ATTiny85 here.
Continue reading this article…
By Assad Ebrahim, on January 3rd, 2010 (157,235 views) |
Topic: Maths--History, Maths--Philosophy
The development of mathematics is intimately interwoven with society and culture, influencing the course of history through its applications to science and technology.
But mathematics itself has changed much over its history. Even the mathematics of the early 1800s can now seem quite strange, so great have been the changes in just the past 150 years as it has been reworked in the modern abstract approach. Though advanced mathematics may now appear arcane from the outside looking in, the present state of mathematics is the result of a natural evolution of the subject. And there is much excitement promised ahead with the rise of new mathematics and application areas in subatomic and quantum physics, in the the field of statistical learning (also called artificial intelligence or machine learning), and in numerical computing and simulation.
What follows is the story of mathematics, in a nutshell.
Continue reading this article…
By Assad Ebrahim, on January 2nd, 2010 (111,134 views) |
Topic: Maths--PhilosophyWhat are the characteristics of mathematics, especially contemporary mathematics?
I’ll consider five groups of characteristics:
- Applicability and Effectiveness,
- Abstraction and Generality,
- Simplicity,
- Logical Derivation, Axiomatic Arrangement,
- Precision, Correctness, Evolution through Dialectic…
Continue reading this article…
|
Stats: 1,089,379 article views since 2010 (Aug '24 update)
Dear Readers: Welcome to the conversation! We publish long-form pieces as well as a curated collection of spotlighted articles covering a broader range of topics. Notifications for new long-form articles are through the feeds (you can join below). We love hearing from you. Feel free to leave your thoughts in comments, or use the contact information to reach us!
|
2,599 feed subscribers
|
