If you haven’t done so already, you may want to start by reading the Preface to the Computing Series: Software as a Force Multiplier, Sections 1-3.
Introducing the LaTeX typsetting platform
If symbols, formulas, and equations comprise a large portion of your professional communication, then you will gain significantly by becoming proficient with the LaTeX (pronounced “lay-tech”) document preparation platform. With the right tools and a little practice, the relative ease of creating beautiful mathematical documents with LaTeX will likely mean that you leave Office in favor of LaTeX for your technical writing.
This article introduces the LaTeX platform (short for Lamport-TeX, after the mathematician Leslie Lamport), illustrates its capabilities, and highlights the key differences between using LaTeX or WYSIWYG “what you see is what you get” word processing systems such as Office.
For those that like to know the human side of the tools they use, we provide a brief history of the legendary TeX (pronounced “tech”) platform, which underpins all variations of which LaTeX is one, looks at the philosophy motivating the development of TeX, and something about its legendary creator Donald Knuth.
 Don Knuth, Leslie Lamport, and an illustration of of why writing mathematics in LaTeX is easier than in Word.
Continue reading this article…
By Assad Ebrahim, on May 20th, 2010 (14,362 views) |
Topic: Maths--Tools, SWEng--Toolbox
(Mathematical Toolset Series: TeX & LaTeX, Part 3 of 3)
If you write frequently, it is likely that you have certain stock or administrative material that is included in each of your documents. You also likely spend a substantial portion of your overall effort re-writing, editing, or re-arranging material. In this situation, one of the best ways of preserving your time and your sanity is to adopt a modular approach to document development.
In this final article of the three part series on LaTeX / TeX, I will discuss a modular approach to document preparation using TeX. I’ll also provide modular templates that should make your use of TeX more efficient.
By Assad Ebrahim, on May 18th, 2010 (22,910 views) |
Topic: Maths--Tools, SWEng--Toolbox
Writing Beautiful Mathematics: Getting Started with LaTeX on Windows
If you haven’t done so already, you may want to start by reading the Preface to the Computing Series: Software as a Force Multiplier, Sections 1-3.
2nd ed. Revised with new templates Sep 21, 2019, 1st ed. May 18, 2010.
Getting Started with LaTex
LaTeX (open source, free) is an essential tool to write beautifully formatted mathematics efficiently. If you have extensive mathematical symbology and have been using MS Word for this, you are using the wrong tool for the job (see Figure below). Setting up LaTeX should take no more than an hour, after which you can produce publication-ready mathematical documents quickly and reliably. This article walks you through setting up a working platform for Windows, and provides the LaTeX templates you’ll need to produce your first examples. Also shared is the source code and compilation instructions for an example paper, which you can download and modify for your own use, containing several advanced stylistic elements (endnotes, figures with captions, URLs, code listings, and epigraphs).
 An example of mathematics written in LaTeX, from Finite Summation of Integer Powers (Part 3), A. Ebrahim, C. Ouellette, 2010. Continue reading this article…
By Assad Ebrahim, on April 15th, 2010 (13,058 views) |
Topic: Education, Maths--Philosophy
An examination of mathematical methods and the search for mathematical meaning.
This article curates a reading list (most sources available freely online) organized into a set of encounters that lie outside the standard mathematics curriculum. They are intended to enrich the reader’s understanding of mathematics and its place in scientific inquiry, increase her/his connection to the historical and philosophical questions behind the mathematics of the past and present, and gain greater satisfaction from further mathematical study. The reader should come away with a better understanding of the culture of mathematics: what mathematics is, mathematical method and meaning, and the relation of mathematics to the empirical world and to science.
We look at seven topics. These may be covered in any order, to suit your particular interests.
- What is Mathematics? (Its Nature and Characteristics)
- Reality, Truth, and the Nature of Mathematical Knowledge
- What is Proof? and the Problem of Certainty
- Some Readings in the History of Mathematics and the Evolution of Its Ideas
- The Search for Foundations in Mathematics
- Mathematics and Science
- Thoughts on Mathematical Practice and Mathematical Style
There is no core body of technical material to master in this course; the important thing is a feel for how, why, and in what context the core ideas of mathematics evolved, getting to the essence of their motivation, and understanding the fruits of these efforts. The course such as the below should appeal to all those who have an itch to scratch beneath the surface of mathematics, who find themselves asking “but why?”. It could be useful in all three tiers of education: secondary, post-secondary (undergraduate), and graduate, appropriately restructured.
- Secondary school elective: to encourage bright students in mathematics, science and technology to enter the university with a broader perspective on the mathematics they will be rapidly learning there.
- University elective course: offered as a writing-intensive seminar, intended primarily for students in the sciences and engineer: mathematics, physics, engineering.
- Graduate level course: offered in the first year of graduate school in mathematics or applied mathematics as a supplementary seminar.
Continue reading this article…
By Assad Ebrahim, on March 14th, 2010 (14,756 views) |
Topic: Maths--General Interest
Data Science & Advanced Analytics
19-21.Oct.2015 (Paris, France)
2015 IEEE International Conference on Data Science & Advanced Analytics (DSAA) will consist of two main tracks, Research and Applications. The Research Track is aimed at collecting contributions related to theoretical foundations of Data Science and Data Analytics. The Applications Track is aimed at collecting contributions related to applications of Data Science and Data Analytics in real life scenarios.
Digital & Web Analytics | Predictive Analytics | Big Data Summits
14-15.May.2014 (London, UK)
At the Bishopsgate Conference Centre in London for this year’s Analytics Innovation Summit.
Booking.com: Data Science
6.Dec.2013 (Amsterdam, Netherlands)
At Booking.com’s head office in Amsterdam, one of the leading players in the eTravel space. The Booking team has a raft of interesting problems in front of them, a bunch of smart, capable data scientists, and a real appetite for applying statistical / machine learning techniques to unlock the next level of benefits. A refreshing visit!
Silicon Milkroundabout 6.0: Analytics
16.Nov, 2013 (London, UK)
At Silicon Milkroundabout 6.0 this weekend. Key question: To what extent are predictive analytics technologies at the heart of the next generation of startups?
(Location: The Old Truman Brewery, 81 Brick Lane, London E1 6QL)
Update:
There are several promising startups in UK’s East End (Silicon Valley lite). The interesting ones (to my mind) were in retail analytics, peer-to-peer lending, even a novel education startup attempting to exploit machine learning techniques. Although the recruitment atmosphere detracts somewhat, SMR is a useful way to assess the next batch of promising start-ups.
Five outstanding startups were:
Predictive Analytics World Conference
23-24.Oct, 2013 (London, UK)
At the Predictive Analytics World Conference for at least part of the Conference, schedule permitting. The programme can be found here: PAW 2013 Programme
Advanced Analytics | Big Data | Hadoop | Social Media | Digital Innovation
30.Apr-1.May, 2013 (London, UK)
At the Advanced Analytics Innovation Summit. This year’s summits are being held at the Lancaster London Hotel, London, UK. (PDF Programme)
(Online Programmes)
Advanced Analytics | Big Data | Hadoop | Social Media | Digital Innovation
Crowd-Source Analytics & Entrepreneurship
9.Mar.2013 (London, UK)
At London Business School discussing the application of advanced data discovery algorithms for a new venture crowd-sourcing business concept.
SAP F&R User Conference
18-19.Sep,2012 (Dresden, Germany)
At the SAP Forecasting & Replenishment User Conference in Dresden, Germany, at the Maritim Hotel & International Congress Centre. This Conference is well attended by senior technical staff from SAF (Simulation, Analysis, and Forecasting) group, which has now become SAP’s Centre of Excellence based out of Schweiz, Switzerland after being acquired by SAP in 2009/2010.
Predictive Analytics & Big Data Innovation Summit
18-19.Apr, 2012 (London, UK)
At the Predictive Analytics & Big Data Innovation Summit. This year, the summit is being held at the Victoria Park Plaza Hotel, London, UK.
Predictive Analytics Innovation Summit
2.Jun & 3.Jun, 2011 (London, UK)
At the Predictive Analytics Innovation Summit (Jumeirah Carlton Towers, Knightsbridge, London, UK).
Third Aladdin (Autonomous Learning Agents for Decentralised Data and Information Networks) Symposium
27.Sep.2010 (Farnborough, UK)
At the Third Aladdin Symposium on Autonomous Learning Agents for Decentralised Data and Information Networks (BAE Systems, Park Centre, Farnborough, UK).
Unmanned Underwater Vehicles Showcase (UUVS) 2010
21-22.Sep.2010 (Southampton, UK)
At the Unmanned Underwater Vehicles Showcase (UUVS) 2010 (National Oceanography Centre, Southampton, UK).
Oceanology International 2010
9-11.Mar.2010 (London, UK)
At Oceanology International 2010 (EXCEL Centre, London, UK).
Advisory Committee on Mathematics Education
2.Mar.2010 (London, UK)
At the ACME Conference 2010 (Royal Society, London, UK).
Articles Repository Online
29.Dec.2009
The Articles Repository for Mathematical Science & Technologies is now online.
By Assad Ebrahim, on February 25th, 2010 (50,172 views) |
Topic: Mathematics, Maths--Technical
Updated! February 5, 2017
The value of zero raised to the zero power, 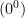 , has been discussed since the time of Euler in the 18th century (1700s). There are three reasonable choices: 1,0, or “indeterminate”. Despite consensus amongst mathematicians that the correct answer is one, computing platforms seem to have reached a variety of conclusions: Google, R, Octave, Ruby, and Microsoft Calculator choose 1; Hexelon Max and TI-36 calculator choose 0; and Maxima and Excel throw an error (indeterminate). In this article, I’ll explain why, for discrete mathematics, the correct answer cannot be anything other than 0^0=1, for reasons that go beyond consistency with the Binomial Theorem (Knuth’s argument).
Continue reading this article…
By Assad Ebrahim, on February 22nd, 2010 (63,853 views) |
Topic: Maths--Tools
If you haven’t done so already, you may want to start by reading the Preface to the Computing Series: Software as a Force Multiplier, Sections 1-3.
Maxima: a Computer Algebra System (CAS) for symbolic computation
Last updated: Feb 19, 2023 (fixed links). Nov 11, 2022 (added omega-math’s excellent web interface, and generating function calculation of the partition of integers problem).
Maxima is a computer algebra system (CAS) for symbolic computation that is free, open source, runs on multiple operating systems (Win,Mac,Linux), and covers a wide range of mathematical capabilities and graphical capabilities. These include algebraic simplification, polynomials, methods from calculus, matrix equations, differential equations, number theory, combinatorics, hypergeometric functions, tensors, gravitational physics, PDEs, nonlinear systems, plus including 2-D/3-D plotting and animation. With a large and responsive user community, there is plenty of help to get up the learning curve, and with its active developer base, Maxima and its ecosystem continue to gain capability, including a fantastic web interface by Omega-Math/Vroom-Labs (see the screenshot below, r0*0). The result is a free, versatile, powerful mathematical computing package for engineers, scientists, mathematicians, programmers, and students. This article will help you get started with Maxima and set you up with resources to flatten the learning curve.
 Omega-Math’s web interface to Maxima. Used here to calculate the first 10 elements of p(n), the number of ways to partition integer n, using a generating function comprising a truncated series of polynomials up to degree n=10
By Assad Ebrahim, on January 31st, 2010 (8,439 views) |
Topic: Education, Maths--Philosophy
The mathematician Alfred North Whitehead observed that “[Advancement occurs] by extending the number of important operations which we can perform without thinking of them.” (Introduction to Mathematics, 1911 ) This is certainly true in mathematics where the development of judicious notation, accompanied by good mathematical technique, extends the capability to perform chains of complex reasoning accurately and efficiently. Through proper problem formulation (tractable yet generalizable), one can sometimes pass from a single insight to the solution of a family of problems, and in some cases, to the solution to the general question itself.
Here, mathematical computing can provide a useful benefit: helping to efficiently explore conjectures, dispatch with false directions, and save time during the development, error-checking and validation stages of obtaining general results. In industry, where specific or semi-general results are needed fast, such tools allow rapidly working up the required material and providing the necessary certainty before the fully general results or complete proof are ready.
Continue reading this article…
By Assad Ebrahim, on January 15th, 2010 (13,435 views) |
Topic: Maths--History, Maths--Philosophy
The development of mathematics has had many encouraging forces: societal, technological, cultural. These have served to accelerate mathematics and have been accelerated in turn, in many cases the pair becoming locked into a mutually beneficial resonance that has dramatically energized both.
In this article, I look at some of the significant catalysts, from the rise of the leisured class in ancient times to the impact of computing in modern times.
Continue reading this article…
By Assad Ebrahim, on January 3rd, 2010 (157,438 views) |
Topic: Maths--History, Maths--Philosophy
The development of mathematics is intimately interwoven with society and culture, influencing the course of history through its applications to science and technology.
But mathematics itself has changed much over its history. Even the mathematics of the early 1800s can now seem quite strange, so great have been the changes in just the past 150 years as it has been reworked in the modern abstract approach. Though advanced mathematics may now appear arcane from the outside looking in, the present state of mathematics is the result of a natural evolution of the subject. And there is much excitement promised ahead with the rise of new mathematics and application areas in subatomic and quantum physics, in the the field of statistical learning (also called artificial intelligence or machine learning), and in numerical computing and simulation.
What follows is the story of mathematics, in a nutshell.
Continue reading this article…
|
Stats: 1,089,379 article views since 2010 (Aug '24 update)
Dear Readers: Welcome to the conversation! We publish long-form pieces as well as a curated collection of spotlighted articles covering a broader range of topics. Notifications for new long-form articles are through the feeds (you can join below). We love hearing from you. Feel free to leave your thoughts in comments, or use the contact information to reach us!
|
